Ο έρωτας δεν είναι μαθηματικά, είναι έμπνευση, είναι αίσθημα, είναι όνειρο. Αυτό ξέραμε ως τώρα και βάσει αυτού πορευόμασταν, κουτσά-στραβά, στο μονοπάτι, που ποτέ δεν ξέρεις πού θα σε βγάλει. Ποτέ; Μπορεί και να ξέρεις ή να μαντεύεις.

Σύμφωνα με τη γενική εμπειρία, ο έρωτας σε μία σχέση γεννιέται και πεθαίνει, περίπου στα τρία χρόνια, αν όλα πάνε καλά ως τότε. Μετά, όταν πεθαίνει, δίνει τη θέση του σε κάτι άλλο. Πες το αγάπη, πες το συνήθεια, πες το ανάγκη, πες το ισορροπία.

Μαθαίνεις να ζεις με αυτόν που ερωτεύτηκες και πλέον μπορεί να σε συνδέουν κι άλλα πράγματα μαζί του πέρα από την επιθυμία για σεξουαλική επαφή. Σε συνδέει ένα κοινό όραμα για τη ζωή: είτε αυτό είναι τα παιδιά είτε είναι κάτι άλλο. Εχετε μάθει να αγαπάτε τα ίδια πράγματα, έχετε αναπτύξει κοινό κώδικα επικοινωνίας, έχετε μάθει να συζητάτε και να λύνετε μαζί τα προβλήματα της καθημερινότητας. Ολα αυτά είναι σχέση και αυτή η σχέση μπορεί να κρατήσει για πάντα.

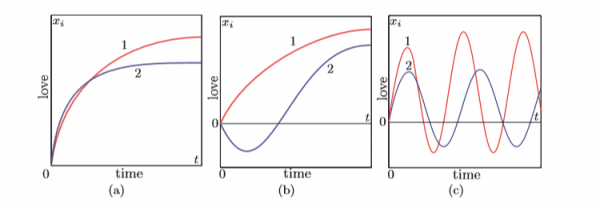
Αυτό λοιπόν, οι μαθηματικοί το εξηγούν με γράφημα. Ο χ και η ψ γνωρίζονται στο σημείο 0. Αρχίζουν να ερωτεύονται οπότε η καμπύλη της σχέσης τους ανεβαίνει. Μετά φεύγει ο έρωτας και η καμπύλη γίνεται ευθεία.

Οταν οι μαθηματικοί βάζουν ευθεία γραμμή στο σχεδιάγραμμα αυτό σημαίνει ότι η σχέση μπορεί να κρατήσει για πάντα

Αν η καμπύλη ξαφνικά πέσει, σημαίνει ότι κάτι δεν πάει καλά – τρίτο πρόσωπο, τάση ανταγωνισμού μέσα στη σχέση, αδιαφορία του ενός ή και των δύο κ.ο.κ. Αν η καμπύλη ξανανέβει, το πρόβλημα ξεπεράστηκε. Ξεπεράστηκε όμως και από τους δύο; Στη μαθηματική πραγματικότητα, βάσει των εξισώσεων, ο ένας από τους δύο δεν το ξεπερνάει. Π.χ. στην περίπτωση τρίτου προσώπου, μπορεί αυτό κάποια στιγμή να εκλείψει και η σχέση του αρχικού ζευγαριού να συνεχιστεί. Ωστόσο η καμπύλη του προσώπου που απάτησε, δεν επανέρχεται εκεί που βρισκόταν πριν την απαγορευμένη σχέση. Αυτό σημαίνει πως αν το έτερον ήμισυ παρουσιάσει κάποιου είδους κλυδωνισμό, ακόμα και μετά την αποχώρηση του τρίτου προσώπου, τότε η σχέση απειλείται, έστω κι αν αυτός που είχε απατήσει τώρα δεν θέλει να χωρίσουν.

 

Ωστόσο σύμφωνα με τα παραδείγματα που παρουσιάζει το σύγγραμμα «Modeling Love Dynamics» που εξέδωσε ομάδα μαθηματικών από το Πολυτεχνείο του Μιλάνου, με επικεφαλής τον καθηγητή Σέτζιο Ρινάλντι, υπάρχουν και περιπτώσεις ερώτων που δεν άρχισαν σαν έρωτες αλλά που κατέληξαν ως τέτοιοι.

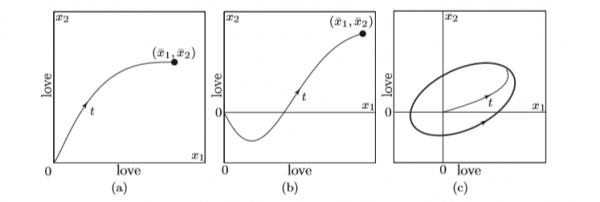
Για παράδειγμα δύο άνθρωποι στην αρχή, έλκονται μεν, αλλά δεν είναι ιδιαιτέρως ενθουσιώδεις. Κατόπιν, καθώς η γνωριμία προχωράει βρίσκουν ή αναπτύσσουν περισσότερα κοινά μεταξύ τους. Τότε οι δύο καμπύλες χ και ψ δείχνουν να έρχονται κοντά. Μετά αναπτύσσεται στενότερη σχέση και προκύπτει έρωτας. Οι καμπύλες μαζί ακολουθούν ανοδική πορεία. Και μετά φεύγει ο έρωτας και έρχεται η άλλη κατάσταση, η σταθερή και συντροφική. Τότε η γραμμή γίνεται ευθεία. Οταν οι μαθηματικοί βάζουν ευθεία γραμμή στο σχεδιάγραμμα αυτό σημαίνει ότι η σχέση μπορεί να κρατήσει για πάντα.

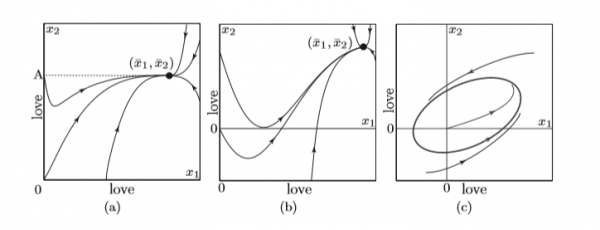
Αλλη περίπτωση γραφήματος είναι η κυκλική σχέση ή η σχέση εκείνων που δεν συναντιούνται ποτέ. Εδώ έχουμε δύο ανθρώπους που λειτουργούν ανταγωνιστικά. Μπορεί μεταξύ τους να υπάρχει πάθος, υπάρχει όμως και τάση του ενός να υποτάξει τον άλλο ή να υπερισχύσει του άλλου και επίσης υπάρχει ένταση. Ενα τέτοιο ζευγάρι στον κινηματογράφο ήταν ο Ρετ Μπάτλερ και η Σκάρλετ Ο’ Χάρα στο «Οσα παίρνει ο άνεμος». Εμοιαζαν να είναι το ιδανικό ζευγάρι όμως ο καθένας ήθελε κατά βάθος άλλα πράγματα και επίσης ο καθένας ήθελε να επικρατήσει η δική του ισχύς σε βάρος του άλλου. Ηταν και οι δύο ανταγωνιστικοί, ήθελαν και οι δύο να επιβληθούν και τελικά δεν μπόρεσαν να αναπτύξουν κοινά σημεία στη συμβίωσή τους. Ως τέτοιο σημείο δεν μπόρεσε να λειτουργήσει ούτε καν η μικρή κόρη τους. Ετσι όταν εκείνη πέθανε ο Ρετ εγκατέλειψε τη Σκάρλετ. Και τότε, που εκείνη ‒είτε από ανασφάλεια, είτε από ανταγωνισμό‒ του αποκάλυψε την ανησυχία της για το τι θα απογίνει χωρίς αυτόν, έλαβε ως απάντηση την πιο σκληρή ερωτική ατάκα στην ιστορία του κινηματογράφου:

«Ειλικρινά αγαπητή μου, δεν δίνω δεκάρα».

Τόσο ωραίο ζευγάρι και να πάει χαμένο; Κι όμως. Η Σκάρλετ απέτυχε, σύμφωνα με τους μιλανέζους μαθηματικούς. Το ίδιο και ο Ρετ. Ακόμα κι αν τα ξαναέβρισκαν, οι εξισώσεις και τα σχεδιαγράμματα δεν θα τους έδιναν πολύ μέλλον.

Αντίθετα, για πιο προβληματικές περιπτώσεις ερώτων όπως π.χ. ο Σιρανό ντε Μπερζεράκ και η Ρωξάνη, στις οποίες όμως δεν υπάρχει ανταγωνισμός, οι μαθηματικοί θα έδιναν περισσότερες πιθανότητες επιτυχίας.

Ο Σιρανό ήταν δύσμορφος. Ετσι, κρύφτηκε πίσω από το όμορφο πρόσωπο του Κριστιάν ντε Νεβιλέτ και έγραφε τις ρομαντικές, ερωτικές επιστολές του στη Ρωξάνη, υπογράφοντας ως Κριστιάν. Στο μυθιστόρημα του Εντμόν Ροστάν, το ζευγάρι δεν ενώνεται ποτέ. Η Ρωξάνη συνειδητοποιεί ότι ερωτεύθηκε τις επιστολές και όχι εκείνον που νόμιζε ότι τις έγραφε και ο Σιρανό δεν της αποκάλυψε ποτέ την αλήθεια.

Αν όμως τελικά οι δύο τους γίνονταν κάποτε ζευγάρι, σύμφωνα με τους μαθηματικούς θα ταίριαζαν στη δεύτερη περίπτωση καμπύλης. Σε εκείνη δηλαδή όπου η σχέση καλλιεργείται προτού χτιστεί ο έρωτας και από τις δύο πλευρές. Η σχέση χτίζεται όμως τελικά σε γερές βάσεις κι έτσι διαρκεί για πολύ και θεωρείται πετυχημένη.

Ενα ακόμα μοιραίο κινηματογραφικό ζευγάρι που θα είχε πολύ μέλλον, αν το μετρήσουμε με εξισώσεις είναι ο Τζακ και η Ρόουζ από τον «Τιτανικό». Η κοινωνική διαφορά που τους χωρίζει είναι μεν τεράστια αλλά η ερωτική έλξη είναι τόσο έντονη και τόσο καθόλου ανταγωνιστική ώστε οι δυο τους, αν δεν έπεφταν πάνω στο παγόβουνο, μάλλον θα παρέμεναν μαζί για πάντα.

Τέλος, για να επιστρέψουμε στις ανταγωνιστικές σχέσεις που κάνουν κύκλους στα γραφήματα και καταλήγουν σε άλυτες εξισώσεις, ας δούμε και την περίπτωση του μοιραίου ερωτικού τριγώνου στην ταινία «Ζυλ και Τζιμ» του Φρανσουά Τριφό. Ο Ζυλ και ο Τζιμ είναι φίλοι και γνωρίζουν την Κατρίν (Ζαν Μορό). Την ερωτεύονται και οι δύο αλλά εκείνη παντρεύεται τον Ζυλ. Αργότερα τα φτιάχνει με τον Τζιμ. Μετά τα ξαναφτιάχνει με τον Ζυλ. Τελικά ο Τζιμ παντρεύεται άλλη γυναίκα. Και μια μέρα, η Κατρίν τον παρασύρει στο αυτοκίνητό της και αυτοκτονεί, σκοτώνοντας και εκείνον. Ο Ζυλ είδε την καταστροφή από μακριά και έμεινε μόνος, να διαχειριστεί τις στάχτες της γυναίκας και του φίλου του.

Πώς να μην μπλοκάρουν οι εξισώσεις με τέτοιο μπέρδεμα; Οι μαθηματικοί λένε ότι η μόνη σχέση που θα μπορούσε να διαρκέσει σ’ αυτό το τρίγωνο αν δεν τους προλάβαινε ο θάνατος ήταν η φιλία μεταξύ του Ζυλ και του Τζιμ. Ομως εδώ το θέμα είναι ο έρωτας, και το γεγονός ότι αυτός δεν χωράει σε κανένα καλούπι, γράφημα ή εξίσωση.

Ακολουθήστε το Protagon στο Google News